Fatigue Analysis, Damage Calculation, and Rainflow Counting in DewesoftX

Course overview

This course enables engineers to perform in-depth fatigue analysis of structural components subjected to cyclic loadings. Starting with fatigue basics, it introduces S‑N curves and the endurance limit, essential for predicting fatigue life and avoiding failures under repeated stress.

You’ll learn to set up and use DewesoftX’s Fatigue Analysis module, where you can filter input signals to eliminate insignificant cycles using rainflow/hysteresis filters and choose between Markov and Rainflow counting methods for accurate cycle detection  . The course covers visual representation tools like range histograms, from/to and range/mean matrices, enabling clear insight into cycle distributions and loading patterns.

Further modules teach how to apply Palmgren‑Miner damage calculation, summing damage across cycle amplitudes using S‑N models  . You’ll explore live monitoring of damage accumulation and offline recalculation during post-processing, ensuring result accuracy.

Finally, you’ll export results—cycle counts, damage summaries, and visual plots—for durability reports or integration into CAE environments, making this course ideal for fatigue engineers, durability analysts, and test professionals working in structural testing. By the end, you’ll be empowered to turn raw cyclic data into solid fatigue life assessments using DewesoftX.

Before diving into the details of fatigue analysis, let us consider the following example. Suppose we want to break a metal rod that is not too thick. How would we approach this task—using brute force like the person in the picture below, or in another way? A fatigue analysis expert would probably suggest repeatedly bending both ends of the rod slightly upward and downward. And they would be right. The rod would eventually break—not necessarily immediately, not after one hundred repetitions, and perhaps not even after one thousand repetitions—but eventually, it would fail.

How can we explain this phenomenon? Let us first describe the physics behind bending the rod. As depicted in the image below, bending induces stress (σ) in the cross-section of the rod. Bending the rod upward induces positive stress, meaning compression at the top and tension at the bottom of the cross-section (a), whereas bending the rod downward induces negative stress, meaning tension at the top and compression at the bottom of the cross-section (b). When the rod is in its equilibrium position, no stress is induced (c).

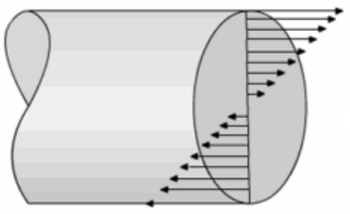
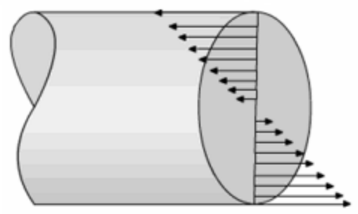
When bending is repeatedly applied over a sufficient period, microscopic cracks are initiated in the cross-section of the rod. As bending continues, these tiny cracks propagate until they grow to a point where the rod breaks. This phenomenon is called crack propagation.

As depicted in the figure below, cracks can propagate in three different modes depending on the relative orientation of the load.

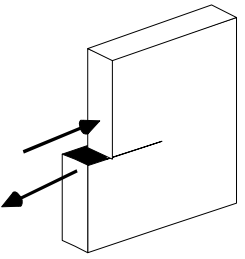
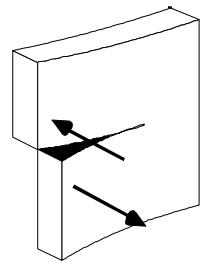
You probably don’t care much about the broken rod in the example above, right? But what if the same rod were part of a larger, more complex structure, such as a bridge, an airplane, or a train, and its fracture could cause a severe accident involving people? Clearly, crack propagation poses serious challenges in both design and analysis across many fields of engineering, especially in civil engineering, where safety is of paramount importance. What makes crack propagation even more problematic is that it is very difficult to detect and measure explicitly. Therefore, fatigue analysis engineers typically rely on implicit statistical and predictive tools, which are described in the following chapters.

In this chapter, we introduce some basic terms used in fatigue analysis and provide a brief overview of the fundamentals.

Load

A load is defined as any physical quantity that represents the excitation or behavior of a system or component over time. The most common types of loads are:

• forces,

• torques,

• stresses,

• strains,

• displacements,

• velocities,

• accelerations etc.

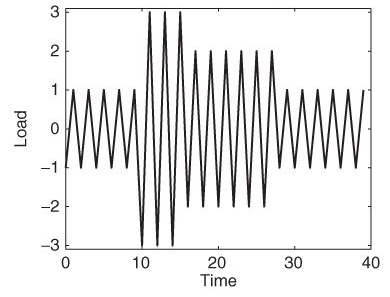
An example of a load signal is shown in the figure below, representing the vertical load measured on a truck transporting gravel. Variations in the mean occur when the truck is loaded or unloaded, while changes in the standard deviation result from differences in road quality.

Cycle

A half-cycle consists of two consecutive extrema in the load signal, going from a minimum to a maximum or vice versa, as shown in Figure 10 below. A full-cycle is composed of two consecutive half-cycles, as illustrated in Figure 11 below.

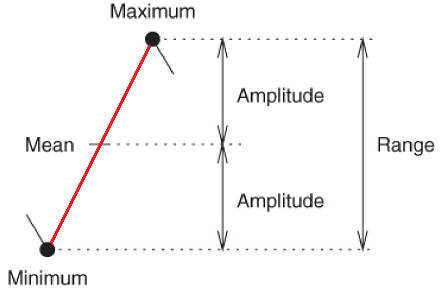
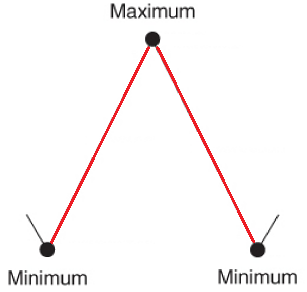
The most important cycle characteristics are Range, Amplitude, and Mean, which are defined as follows:

• Amplitude = (Maximum - Minimum) / 2,

• Range = Maximum - Minimum,

• Mean = (Maximum + Minimum) / 2.

Cycle counting methods

Cycle counting methods are used to calculate the load spectrum of a load signal, that is, the number of cycles corresponding to each range in the signal. An example of a load spectrum is shown in the figure below. Typical cycle counting methods include rainflow counting and Markov counting, which are described in the following chapters.

Fatigue

Fatigue is a failure mechanism caused by repeated load cycles with amplitudes well below the material’s ultimate static strength. Formally, the fatigue process is divided into three stages:

• crack initiation,

• crack propagation,

• unstable rupture and final fracture.

• load type,

• object size

• stress/strain concentration and distribution,

• mean stress/strain,

• environmental effects,

• metallurgical factors and material properties,

• load rate and frequency effects.

Fatigue life prediction

Fatigue life prediction is the process of estimating the fatigue life of a particular object under observation. According to ASTM, fatigue life is defined as the number of stress cycles that a specimen can sustain before failure. Predicting fatigue life is of vital importance to ensure product quality and safety.

Durability

Durability is the ability of an item to withstand its intended use over a sufficiently long period of time. Good durability contributes to high quality, company profitability, and customer satisfaction.

Generally speaking, S-N curves (also known as Wöhler curves) represent statistical models that characterize material performance. An S-N curve is defined as a graph of cyclic stress versus the logarithmic scale of cycles to failure. The figure below depicts two S-N curves—a red one and a blue one—corresponding to aluminum and steel, respectively.

Let us take a closer look at the latter. If a cyclic stress of approximately 45 ksi* is applied to the steel, failure will occur after 10⁴ cycles, whereas applying a lower cyclic stress of approximately 40 ksi will result in failure after 10⁵ cycles. Furthermore, at 30 ksi, the S-N curve reaches the so-called endurance limit, which is the amplitude of cyclic stress that can be applied to the material without causing fatigue failure. Thus, if a cyclic stress of 30 ksi or less is applied to the steel, failure will never occur. On the other hand, at 45 ksi, the S-N curve reaches the so-called ultimate stress, defined as the maximum stress a material can withstand.

S-N curves are derived from tests on material samples, called coupons, where a regular sinusoidal stress is applied by a testing machine that also counts the number of cycles to failure, as depicted in figures (a), (b), and (c) below. This process is known as coupon testing. Each coupon test generates a point on the plot; however, in some cases, there is a run-out, where the time to failure exceeds the available test period. Analysis of fatigue data requires techniques from statistics, particularly survival analysis and linear regression.

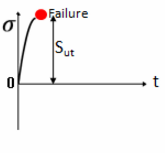
When designing components, engineers always aim to keep stress amplitudes below the endurance limit, well below the ultimate stress value. Since the material does not fail below the endurance limit, it is safe to operate at such stress amplitudes.

The S-N curve model described in the previous chapter assumes that the material is subjected to a constant-amplitude load, meaning that cycles to failure correspond to a constant cyclic stress amplitude, as shown in Figure 17 below. A further generalization is to consider a block load, which consists of consecutive blocks of constant-amplitude load, as illustrated in Figure 18 below.

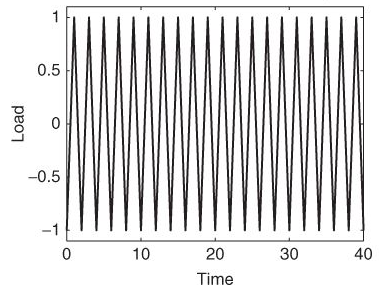
In this case, the Palmgren-Miner damage accumulation hypothesis states that each cycle with amplitude SiS_iSi​ consumes a fraction 1/Ni1 / N_i1/Ni​ of the total life. Thus, the total fatigue damage DDD is given by the following equation:

where nin_ini​ is the number of cycles with amplitude SiS_iSi​. Fatigue failure occurs when the damage DDD exceeds one.

Although the Palmgren-Miner rule represents a useful approximation model in many circumstances, it has several major limitations:

1. It fails to account for the probabilistic nature of fatigue.

2. In some cases, cycles of low stress followed by high stress cause more damage than the rule predicts. The rule does not consider the effects of an overload or high stress, which may result in compressive residual stress that can retard crack growth. Conversely, high stress followed by low stress may cause less damage due to the presence of compressive residual stress.

Although fatigue analysis covers a broad range of areas, such as mechanics, physics, and statistics, it can be simply defined as the process of analyzing, modeling, and predicting fatigue behavior. To summarize the basics of fatigue analysis, let us consider a simple example illustrating its application in the automotive industry.

Suppose a company—or one of its divisions—is manufacturing drive shafts, and a team of engineers is responsible for ensuring they meet performance, quality, and safety requirements. Assuming that preliminary drive shaft tests have already been performed and the team is now focused on long-term analysis, what would be the next steps?

Typically, the engineering team would first gather as much statistical data as possible, including the target driver group (e.g., whether the shafts will be used in family cars, trucks, etc.), target driver behavior (average driving distance per year, average driving speed, etc.), and target driving conditions (road conditions, speed limits, etc.). Based on this information, statistical models describing the target environment would be developed. These models would then guide real-life testing, including driving under actual conditions, with all necessary data acquisition taking place, such as measuring the loads applied to the drive shafts.

Finally, cycle counting methods would be applied to the measured load signals, and statistical tools, such as S-N curves or the Palmgren-Miner rule, would be used to determine whether load amplitudes exceed the steel’s endurance limits, how often and by how much they exceed them, whether the fatigue limit is surpassed, and whether Palmgren-Miner damage accumulates beyond acceptable levels. If the results do not comply with the recommended values, the shafts would likely require additional modifications and re-engineering.

The Fatigue Analysis Module supports a wide range of fatigue analysis features and utilities. When combined with DewesoftX, it provides a powerful all-in-one fatigue analysis solution, enabling both acquisition and analysis of fatigue data—everything in a single software package!

It is located under Strain → Stress → Fatigue Analysis.

The module is organized into three main sections: Preprocessing, Counting Methods (Algorithm Settings), and Visualization. This organization follows a typical fatigue analysis workflow, starting with input signal preprocessing, proceeding with cycle counting, and ending with result visualization.

Each section represents a specific stage of fatigue analysis and covers a corresponding subset of methods as follows:

1. Preprocessing

   • Turning points filter

   • Rainflow filter

   • Discretization filter

2. Counting methods

   • Rainflow counting (ASTM E 1049-85)

   • Markov counting

3. Visualization

   • Range histograms

   • From/to matrices

   • Range/mean matrices

4. Damage calculation

• Accumulated damage (Palmgren-Miner rule)

The Preprocessing section includes the Turning Points filter, Rainflow filter, and Discretization filter.

Turning points filter

The Turning Points filter detects local extrema, namely turning points, in the load signal. An example of turning point detection is shown in Figure (a) below. This filter is applied to the input signal by default and cannot be disabled, as the Fatigue Analysis Module requires a sequence of turning points as its input rather than the full load signal.

Rainflow filter

The Rainflow filter (also called the hysteresis filter) removes small oscillations from the signal, as shown in Figure (b) below. All turning points corresponding to cycles with ranges below a given threshold are removed. The higher the threshold, the more turning points are filtered out, and vice versa. Rainflow filtering can significantly reduce the number of turning points, which is important for both testing and numerical simulation. The Threshold parameter, with value T, corresponds to T% of the absolute load signal range.

Discretization filter

The Discretization filter divides the range of a load signal into N equidistant bins and assigns each turning point to its closest bin. Figure (c) below shows an example in which a signal ranging from -10 to 10 is discretized into 5 bins. Load signals are typically highly stochastic (please refer to the first figure in the Fatigue Analysis Basics chapter); therefore, discretization is often applied to make them smoother and less stochastic. The number of bins is adjusted using the Class Count parameter.

Both the Rainflow filter and the Discretization filter can be activated in the Preprocessing section by selecting the appropriate checkboxes, as shown below.

Description of the Markov Counting Method

Markov counting is one of the most straightforward cycle counting methods. It operates on consecutive pairs of turning points and calculates the absolute ranges between them. The method is activated by selecting the Markov Counting checkbox in the Algorithm Settings section.

The figure below illustrates an example of Markov counting in action. The 6th turning point of the load signal is assigned a value of |5 − 2| = 3, which represents the absolute difference between the 6th and 5th turning points. Similarly, the 7th turning point is assigned a value of |4 − 5| = 1, corresponding to the absolute difference between the 7th and 6th turning points.

When large-amplitude cycles (such as the cycle between the 5th and 8th turning points in the figure above) contain smaller-amplitude cycles, Markov counting fails to detect the smaller ones. Since large-amplitude cycles play a critical role in fatigue life, this represents a significant limitation of the method.

Rainflow counting is generally recognized as the most effective cycle counting method to date and has become the de facto industrial standard. It is activated by ticking the Rainflow counting checkbox in the Algorithm settings section.

The idea behind the method is to detect hysteresis loops in the load signal, as shown in the figure below. These hysteresis loops will be referred to as closed cycles. Portions of the signal that do not correspond to closed cycles are called open cycles or residuals. In simple terms, closed cycles and residuals can be visualized as full cycles and half cycles, respectively.

In contrast to Markov counting, which fails to detect large amplitude cycles, rainflow counting successfully identifies them. As shown in the figure below, it detects the large amplitude cycle (2,6) as well as the small amplitude cycle (4,5) within it.

Different rainflow counting standards, such as ASTM, DIN, and AFNOR, vary in their treatment of residuals. To ensure maximum flexibility, the Fatigue Analysis Module supports both residual and non-residual modes. When the Ignore residuals checkbox in the Additional algorithm settings section is selected, residuals are omitted; otherwise, they are included in the results.

To graphically represent the results, the Fatigue Analysis Module uses the most common visualization techniques in fatigue analysis: range histograms, from/to matrices, and range/mean matrices. When an input channel corresponding to a load signal of interest is selected, the following new channels are created:

• Preprocessing

  • Peak/valley channel

  • RF filter channel

  • Discretization channel

• Rainflow counting

  • Range histogram channel (2-D)

  • Range/mean matrix channel (3-D)

  • From/to matrix channel (3-D)

• Markov counting

  • Range histogram channel (2-D)

  • From/to matrix channel (3-D)

All the channels are shown in the screenshot below.

A range histogram is a 2-D graph representing the range distribution of a load signal. An example of a range histogram is shown in the figure below. The X-axis and Y-axis correspond to the range and the number of cycles, respectively. For example, if a load signal contains 500 cycles with a range of 20 and 700 cycles with a range of 40, the points (X=20, Y=500) and (X=40, Y=700) would be plotted on the range histogram.

A typical use case for a range histogram is to obtain the histogram of a signal, rotate it along the diagonal (swapping the X-axis and Y-axis), overlay the corresponding S-N curve, and check whether the data remain well below the curve.

The From/To Matrix is a 3D graph representing the cycle distribution of a load signal. An example of a From/To Matrix is shown in the image below.

• X-axis - From (cycle minimum)

• Y-axis - To (cycle maximum)

• Z-axis - Number of cycles

For example, the image below shows a cycle ranging from 5 to 10. In this case, From and To are assigned the values 5 and 10, respectively. If a load signal contains 100 such cycles, an entry of (X=5, Y=10, Z=100) would be added to the From/To Matrix.

The range/mean matrix is a 3D graph representing the cycle distribution of a load signal. An example of a range/mean matrix is shown in the figure below.

• X-axis - cycle range

• Y-axis - cycle mean 

• Z-axis - number of cycles

For a detailed description of cycle range and cycle mean, please refer to the Fatigue Analysis Basics chapter.

For example, the figure below depicts a cycle ranging from 5 to 10. In this case, the range is calculated as 10 − 5 = 5, and the mean is calculated as (10 + 5) / 2 = 7.5. If a load signal contained 300 such cycles, an entry of (X = 5, Y = 7.5, Z = 300) would be added to the range/mean matrix.

The visualization section is organized into three groups: Range, Mean, and From/To, as shown in the screenshot below. Each group controls the appearance of the corresponding graphs. For example, the Range group controls the appearance of the range histograms and the range/mean matrices. The Min range and Max range parameters specify the minimum and maximum values of the range axis, while the Classes parameter specifies the number of classes into which the range is divided.

When the Auto checkbox is selected, Dewesoft automatically calculates the Min range and Max range from the input signal. The same principle applies to the Mean and From/To groups.

The appearance of graphs can also be controlled in the Dewesoft settings window under Extensions > Fatigue Analysis > Settings, as shown in the screenshot below.

The Ticks parameter controls the position of the graph ticks. When Show ticks at class centers is selected, the ticks are displayed exactly at the class centers, whereas Show ticks at lower-class bounds displays them at the lower class bounds, as shown in figures (a) and (b) below, respectively..

Additional Fatigue Analysis Module settings can be found in the Dewesoft settings window under Extensions > Fatigue Analysis, as shown in the screenshot below.

Ticks

For the Ticks parameter, please refer to the Visualization Settings chapter.

Use Hard Drive For Calculation

When analyzing extremely large data files with the Fatigue Analysis Module, the operating system may run out of memory. To increase robustness and avoid such issues, the module supports a special hard drive mode. In this mode, all intermediate data is stored on the hard drive instead of in RAM, substantially reducing memory usage.

The hard drive mode is activated by selecting the Use Hard Drive for Calculation checkbox. However, this mode significantly decreases performance and increases processing times, so it should only be used when out-of-memory problems occur.

In this chapter, we present an example of a complete fatigue analysis workflow using the Fatigue Analysis Module and Dewesoft. We begin with a simple signal, named Stress Data, as shown in the screenshot below. The signal is stochastic and contains several turning points.

First, we activate the Fatigue Analysis Module, located under Strain, Stress → Fatigue Analysis. After activating the module, the setup screen appears, as shown in the image below. We assign an input channel to the module by ticking the Data checkbox on the left-hand side of the screen. No preprocessing will be applied; therefore, the Rainflow Filtering and Discretization checkboxes are left unchecked. To apply both counting methods, we tick the Rainflow Counting and Markov Counting checkboxes.

Next is the visualization. After ticking all three Auto checkboxes, Dewesoft automatically assigns values of 0 and 9 to the Min and Max edit boxes, respectively, since 0 and 9 represent the minimum and maximum of the input signal. For clearer visualization, the Classes parameter is set to 10. Thus, each class has a width of 1, calculated as (9−0+1)/10=1(9 - 0 + 1) / 10 = 1(9−0+1)/10=1. Dividing the range into 11 classes, for instance, would not yield a whole number, since (9−0+1)/11=0.91(9 - 0 + 1) / 11 = 0.91(9−0+1)/11=0.91.

Finally, we navigate to the Review tab and click the Recalculate button. After recalculation, the result screen is displayed, as shown in the image below. The screen contains five graphs: the range histogram and from/to matrix corresponding to Markov counting, and the range histogram, from/to matrix, and range/mean matrix corresponding to Rainflow counting.

The results obtained in the previous chapter can optionally be exported to a wide range of file formats. For example, we can export the data to a text file. To do this, we navigate to the Export tab, as shown in the screenshot below, and select **Text/CSV (.txt, .csv) from the list of supported file types. After choosing the appropriate channels on the right side of the screen, we click the Export button.

When the export is complete, the exported text file appears in the Existing files list box. Double-clicking the file opens it in an external text viewer (such as Notepad), as shown in the screenshot below.

Perform Damage Calculation According to the Palmgren-Miner Rule

According to Miner's Rule, failure occurs when the accumulated damage reaches 1. The definition of failure for a physical part can vary: it may indicate that a crack has initiated on the part’s surface, or that a crack has propagated completely through the part, causing it to separate.

To perform a damage calculation, you must first add an S-N curve in the S-N curve editor.

Please ensure that the input units of the signal match the units of the S-N curve. In the S-N curve editor, you can add a custom S-N curve, specifying its name, units, axis type, and the number of points. Once you have finished defining the curve, click the Save button.

After adding the S-N curve, return to the Fatigue Analysis Module and select the Accumulated Damage option. Once this option is selected, you will be able to access the S-N Curves tab.

The next step is to navigate to the S-N Curves tab and select the appropriate S-N curve.

Only the overall damage within the defined area of the S-N curve will be calculated. If your stress level or the number of cycles falls outside the predefined area, the damage will not be included in the overall calculation.

As shown in the image above, for this specific S-N curve, only the damage calculated from stress levels and cycle numbers within the orange area will be included in the overall damage calculation.